 The TI-Nspire CX & CBR 2
The TI-Nspire CX & CBR 2 "Why is it so important we're able to phrase the distance from an object like that?" I had heard on several occasions. I DID have access to a Texas Instruments TI-Nspire CX as well as their CBR 2 (Calculator-Based Ranger), which had been useful in the past with a ball bounce lab and I fully intend this school year to do the Bungee-Jumping Barbie lesson. With CBR 2 and TI-Nspire CX in hand, I began to collect data in the hallway outside my classroom during a passing period with students walking by at a variety of distances away from the sensor. This was insightful, but did little to give relevance to the idea of absolute value inequalities as I had set out to do.
So after thoroughly banging my head against the drawing board, so to speak, I decided to relate the back-up sensor (and camera) on an automobile to the compound inequalities and absolute value equations we had been investigating earlier in the week.
 She seems to have a lot of faith in my backing skills, huh?
She seems to have a lot of faith in my backing skills, huh? We -- er, actually, I -- backed the vehicle towards our volunteer (pictured here, seen through the vehicle's back window, exercising every ounce of trust she can muster up) and measured her distance to the sensor when it changed intensity and/or volume. The video was simple enough to capture, so I uploaded it to YouTube HERE, if you feel the need to use it in 3-Act-Math format (and because I always enjoy working a Dan Meyer shout-out into a blog post). My intent was to use the video clip as an Act 1, then the photo below for Act 2 to include some accompanying details and measurements. I have not managed, at this time, to accumulate the necessary camera shots for an Act 3, but hope I can do so in the not-too-distant future.
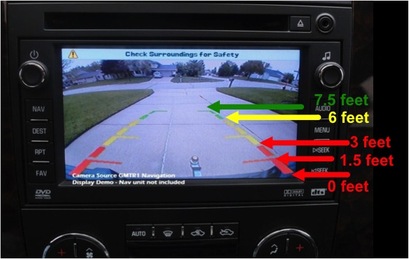 Image reflects data collected from observed alarm-distance relationship.
Image reflects data collected from observed alarm-distance relationship. The prompt I gave students was that they needed to be able to provide enough information about the inequalities associated with each tone, so that we could construct a "poor-man's vehicle backing system." To be fair, earlier in the week, we had created several of our own programs to use with the TI-84 Plus (now available in the TI-84 Plus C with color screen and rechargeable battery, which I've grown to appreciate quickly) calculators, including Quadratic Formula, Distance Formula, Slope Formula, and Midpoint Formula programs. I aim to include links to these files as soon as my school webpage editor is properly troubleshot. For now, you may browse my classroom webpage using THIS link.
While this particular prompt may not fit the ideals for the Common Core State Standards for Mathematics, I feel it does give some worthwhile insight into how computer programming logic has a place in a vital component of vehicle safety systems. Sometimes, this sort of insight is enough to squelch the "But when am I ever going to USE THIS STUFF in real life?" questioning that can occur frequently with math topics.
 If using the 3-Act Math format, this could serve as Act 3 for the time being. Sorry.
If using the 3-Act Math format, this could serve as Act 3 for the time being. Sorry. Most importantly, I wanted to see that students had the wherewithal (yes, I used "wherewithal" in context on a math blog entry) to only include, for example, "6 feet" as part of a single interval instead of assigning it to more than one interval. My hopes in this was to have some sort of reinforcing example to refer to when we begin our look at functions and how each input value can only have one output value.
The female student in the video seems pretty bold to stand firm, knowing that I'm backing up straight towards her and, truth be told, there was a Counselor's meeting going on while we were filming in the conference room directly behind her. So, I had some explaining to do when I ran across a couple of those counselors towards the end of the school day, but did get some head nodding and encouragement that the lesson potential for what I was doing sounded pretty interesting to them.
In conclusion, this lesson has been the most fun I've had ALMOST intentionally backing over a student in my teaching career. Just wanted to put that out there. Please let me know your thoughts on this lesson and check my Twitter feed to see when I've been able to post those TI-84 programs, if you are interested in when I have those posted. Thanks!
--Keltner--

 RSS Feed
RSS Feed